1. Introducción

En el curso de Tópicos Avanzados de Inteligencia Artificial de la Universidad de Sonora se propuso aprender a realizar un reconocedor de voz. Todos teníamos idea de algunas de las partes que lo conformarían: yo, por ejemplo, sabía que tendríamos que hacer y entrenar modelos de lenguaje para interpretar correctamente lo que obteníamos del audio. Sin embargo, creo que nadie pensó qué tantas partes conforman a un reconocedor de voz. En este blog pienso hablar de todas las herramientas que necesitamos para hacer un reconocedor de voz desde cero. En la siguiente sección hablaremos de métricas para evaluar nuestro reconocedor de voz (qué tan bueno es nuestro reconocimiento del habla). Después en la sección 3 vamos a hablar de cómo la voz es transmitida y llega a algún micrófono para después ser procesada y representada adecuadamente para ser utilizada en algoritmos de reconocimiento. En las secciones 4 y 5 vamos a modelar el reconocedor de voz, para ello lo partiremos en dos: la primera (que detallaremos en la sección 4) es el modelo acústico(MA), que se encarga de la parte de la voz (las señales, frecuencias y magnitudes asociadas a un sonido o uterancia) y cómo representarla y codificarla adecuadamente; mientras que en la segunda (sección 5) definimos el modelo de lenguaje (ML), que nos permitirá calcular cuáles serían las siguientes palabras en una frase sin siquiera haber oído la palabra aún. En la sección 6 hablaremos un poco del pegamento que une estos dos modelos de manera elegante (los trasductores de estado finito).

¿Porqué separarlo asi?

En el estado del arte los sistemas de reconocimiento del habla son un problema de optimización estadística, donde lo que se busca encontrar es la secuencia de palabras $W = \{w_{1}, w_{2}, w_{3}, ... , w_{N}\}$ que mejor represente una secuencia de uterancias emitidas por voz humana. Para lograrlo, tenemos una serie de evidencias $E = \{e_{1}, e_{2}, e_{3}, ... , e_{M}\}$, es decir, que buscamos encontrar una $W$ tal que

donde $P(E\|W)$ es el MA y $P(W)$ son probabilidades a priori que obtendremos de nuestro ML.

2. Primero lo primero: ¿qué queremos conseguir?

Queremos hacer un reconocedor de voz, sí. Pero, ¿cómo y cuándo sabemos que tenemos un reconocedor de voz? ¿Debe de ser perfecto? Antes de emepzar cualquier cosa debemos definir algo muy importante: cómo vamos a evaluar a nuestro sistema. Una de las métricas más utilizadas en los sistemas de reconocimiento del habla es el Word Error Rate (WER), que evalúa a partir del número de veces que pusimos una palabra por otra ($N_{sub}$), el número de palabras que sí se dijeron pero que el sistema de reconocimiento no detectó ($N_{del}$, y el número de veces en las que el sistema puso palabras donde no había ($N_{ins}$), y el número de palabras que se dijeron.

Como habrás sospechado, la métrica WER se calcula de la siguiente manera:

que si lo vemos un poco de cerca no es más que un edit distance normalizado. También se puede hacer lo análogo con oraciones en vez de palabras (SER) o letras (LER).

3. Procesamiento, caracterización y codificación de la voz

Las ondas del sonido de la voz se propaga a través del aire y son capturadas por un micrófono. Después, éste las convierte en actividad eléctrica y ésta es muestreada para crear una secuencia de muestras en forma de onda que describen la señal. Estas ondas de sonido viajan en frecuencias (medidas en Hz o MHz). Particularmente, el sonido de la voz viaja en frecuencias alrededor de los 8,000 Hz. Para representar adecuadamente esta señal (de voz) es necesario hacer el muestreo que hablábamos ante y, para hacerlo, nos podemos auxiliar del teorema de Nyquist, en el cual explica que la frecuencia de muestreo (número de muestras por segundo) debe ser de al menos dos veces la frecuencia de la señal que vamos a digitalizar (es decir, debe ser de 16,000 muestras por segundo el muestreo de voz). De ser menos del doble, habrá partes de la señal que no serán representadas correctamente en la versión digital.

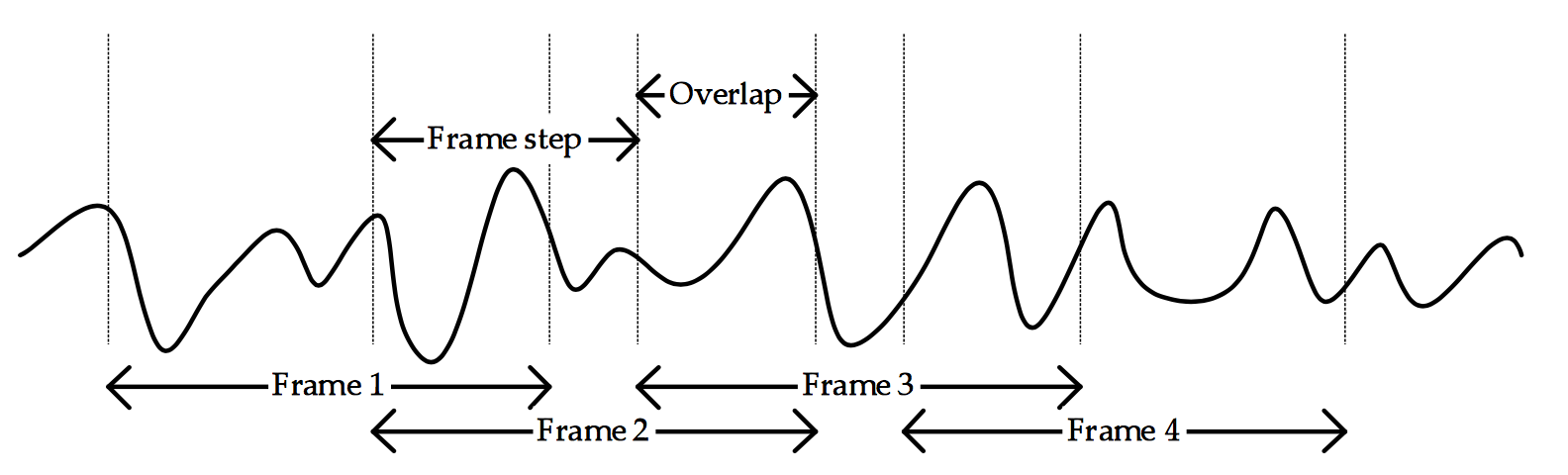
Debe ser evidente para el lector, que las propiedades estadísticas del muestro de la señal son no estacionarias. Es decir, cambia en función del tiempo. Por lo cual, vamos a analizar la señal por tramas o frames lo suficientemente pequeños para poder asumir un sistema estacionario. También debemos tener cuidado con las orillas de las tramas, ya que podríamos perder información importante, es por esto que al representar nuevamente las señales de manera estacionaria también sobrelapamos las tramas unas con otras (usualmente las ventanas o tramas son de 25ms, y las sobrelapaciones son de 10ms para adelante y otros 10ms para atrás).

Después de esto, vamos a transformar cada trama a partir de la Transformada Discreta de Fourier (TDF) y nos quedaremos únicamente con la parte real

Suavizado con filtros de Mel

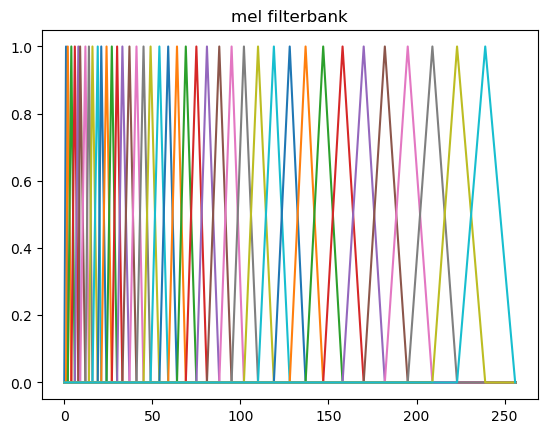
Tenemos una rica codificación de los datos, pero aún no estamos listos para lanzarnos al siguiente paso. ¿Qué es lo que se realiza en la actualidad para evitar los ruidos aleatorios en el silencio, entre otros factores que involucran un peor desempeño, realizamos un suavizado en el espectro de magnitud que obtenemos después de calcular la TDF el cual está motivado en el sentido auditivo humano a partir de filtros. Estos filtros (los de Mel son 40) se aplican a nuestro espectro de magnitud, de manera que dentro de cada uno de los primeros filtros haya un rango muy pequeño de frecuencias, y a mayor frecuencias, mayor será el ancho del filtro, como se puede ver en la siguiente imagen:

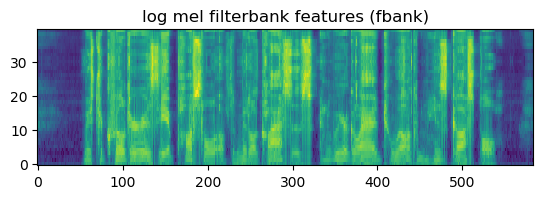
Por último, aplicamos operaciones logarítmicas a nuestro espectro de magnitudes, Esto permite comprimir el rango de señales y también modela mejor lo que ocurre en el sistema auditivo. Al resultado de realizar el logaritmo a nuestro espectro de magnitudes que pasaron por los filtros de mel les llamamos coeficientes del banco de filtros.

4. Modelo acústico

n most systems today, the acoustic model is a hybrid model with uses deep neural networks to create frame-level predictions and then a hidden Markov model to transform these into a sequential prediction. A hidden Markov model (HMM) is a very well-known method for characterizing a discrete-time (sampled) sequence of events. The basic ideas of HMMs are decades old and have been applied to many fields.

El modelo acústico implementado para nuestro reconocedor del habla es un modelo híbrido, el cual usa redes neuronales profundas para crear predicciones a nivel de tramas, y otro modelo para transformar estas predicciones en una secuencia de predicción a través de Modelos Ocultos de Markov (MOM).

Modelos Oculos de Markov

Mucho más conocidos como HMM (por sus siglas Hidden Markov Models) nos permitirán modelar observaciones acústicas a un nivel menor que una palabra, como los fonemas, fonos o senones. Estos últimos serán detallados más adelante. Un HMM es un proceso estocástico con

• Un número finito de estados.
• Transiciones probabilísticas entre estos estados (estocástico).
• El siguiente estado es calculado a partir del estado actual (asunción de Markov de primer orden).
• No podemos saber en qué estado estamos (doblemente estocástico).

Es típico que cada fonema sea representado por un modelo oculto de Markov con tres estados, y luego cada palabra es representada por la concatenación del HMM de cada fonema que compone a la palabra.

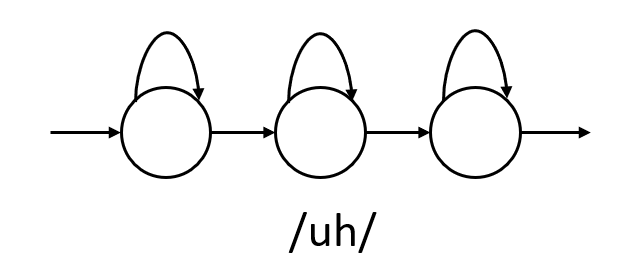
En la imagen anterior, se concatenan los tres fonemas que componen a la palabra “cup” en inglés. Nótese que no siempre tiene que ser una concatenación de tres HMM. Por ejemplo, para modelar la palabara “Víctor” necesitaríamos cinco HMM de tres estados cada uno. Anteriormente, cada estado en los HMM tenía asociada una distribución de probabilidad definida por Modelos de Mezclas Gaussianas (). Sin embargo, en la actualidad se usan redes neuronales profundas para calcular las probabilidades a posteriori de cada uno de los HMM, teniendo una salida para cada estado de cada fonema. En español, por ejemplo, el número de fonemas es de mínimo 22 (fácil de googlear, pero dejo aquí una referencia), es decir que si representamos cada fonema con tres estados, la red neuronal debe tener 66 salidas. En inglés esto difiere bastante, ya que en promedio hay 40 fonemas, es decir, 120 salidas de la red.

Senones

Hasta ahora, la representación de cada fonema ha sido sin considerar el fonema anterior, es decir, independientes del contexto. Sin embargo, en el inglés suena diferente la \a\ que está en BAT a aquella que está en CUP. Esto suele deberse al fono anterior. Por lo que, hace falta modelar de manera diferente (por lo menos en inglés) nuestros fonos. Para ello vamos a utilizar trifonos los cuales no son más que tres fonos consecutivos. Sin embargo, ocurre que para modelar los 40 fonemas diferentes en trifonos ocuparíamos $40^{3}$ HMM, y si cada HMM es de tres estados, entonces ocupamos 192,000 estados por modelar. Esto claramente es un problema. A pesar de esto, en la actualidad existe un apoyo para reducir tal explosión de datos, que son los senones. Un senón es la unión de estados que suenan muy similar en un solo HMM. La obtención de la colección de senones fue posible gracias a un conjunto de reglas predefinidas que permitieron agrupar todos los fonos similares en un sólo senón. El resultado de esto: 10,000 senones que nos permitirán hacer el entrenamiento de nuestro modelo acústico en un sistema dependiente del contexto con redes neuronales, donde la función objetivo típicamente es la entropía y la salida de la red es una capa (obviamente) softmax.

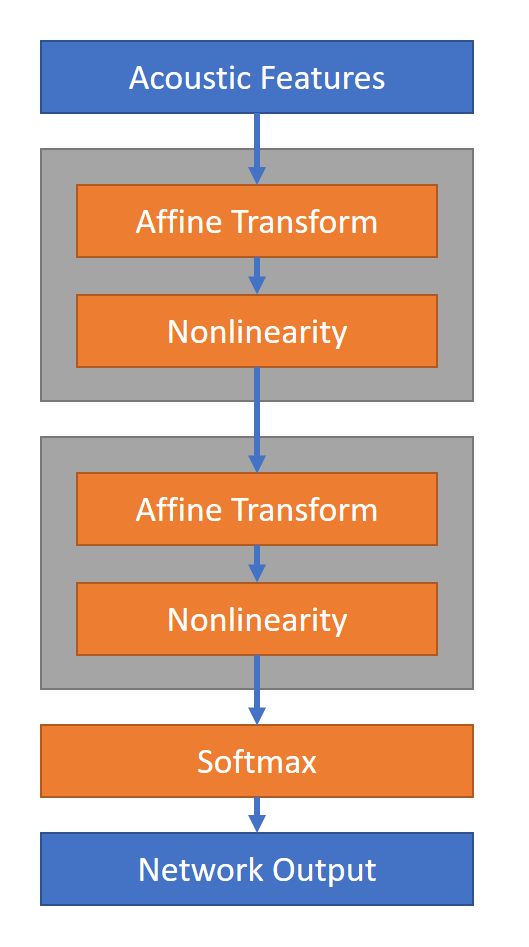
La transformación afín no se refiere más que a una transformación lineal más un un vector $B$. De hecho, la transformación lineal puede verse como un caso particular de la transformación afín; la no linealidad se refiere a la activación RELu en las neuronas. En la actualidad, la arquitectura de red más utilizadas para entrenar el modelo acústico son las redes neuronales recurrentes, en particular las LSTM que permiten que las probabilidades no se acerquen tanto a 0 ni que sean demasiado altas.

5. Modelo de Lenguaje

Recordemos que el modelo del lenguaje es la parte en la que estimamos $P(W)$, es decir, las probabilidades a priori de la secuencias de palabras que representan una frase por voz. El problema parece bastante complejo. Nótese que debemos asignar probabilidades a un conjunto de palabras (de tamaño desconocido) con una longitud de secuencia que va desde 0 hasta otro número desconocido. Es decir, tenemos un número infinito de secuencias de palabras. Para empezar a simplificarlo, vamos a limitar las palabras a través de un vocabulario del modelo de lenguaje. Cuando entrenamos nuestro ML, toda palabra que aparezca en el corpus será parte de nuestro vocabulario. Aquellas que no aparezcan serán conocidas como palabras fuera de vocabulario. Si no está en nuestro vocabulario, entonces será imposible que nuestro reconocedor del habla la considere como una posible palabra dentro de la secuencia.

Representación del lenguaje

Uno de los modelos de lenguaje más conocidos son los N-gramas, los cuales estiman probabilidades para cada secuencia de palabras dentro del vocabulario haciendo uso de la asunción de Markov de N orden. Para un modelo de 1-grama, la probabilidad asociada a cada secuencia de 1-gramas es calculada

Es decir, cada palabra es dependiente sólo de la anterior. Cuando hacemos uso de bigramas, entonces cada palabra es dependiente de sus dos anteriores en una secuencia de palabras, y así para todo n-grama. Debe destacarse que siempre es más adecuado que nuestra N sea lo más grande posible, es decir, un modelo bigrama representa mejor nuestro lenguaje que uno con unigramas. Sin embargo, para N=4 o N=5, es más común que frases de tales longitudes no hayan sido reconocidas las suficientes veces en todo el corpus, por lo tanto, empieza a dar peores resultados. La mejor estrategia para saber cuál es el modelo de lenguaje que mejor resultados dará es a través de la métrica de perplejidad.

Estimar N-gramas

Si buscamos calcular

es decir, la probabilidad de encontrar “es” después del unigrama “Víctor”, entonces tendríamos que calcular

Nótese que tan sólo se trata de calcular el número de veces que aparece la secuencia en todo el corpus, entre las veces que aparece la última palabra.

Suavizado del ML

Houston, tenemos un problema: imaginemos que queremos calcular la probabilidad de la secuencia anterior (“Víctor es”). Resulta que en un corpus la palabra “es” aparece unas 1,000 veces, Víctor aparece unas 500 veces, pero la concatenación de las dos no aparece ni una vez. Es decir, que la probabilidad asociada es 0. Tiene sentido desde la perspectiva en la que los datos de entrenamiento deben ser la mejor representación de aquello con lo que vamos a entrenar (no vamos a entrenar con un corpus en español, para luego clasificar textos en chino). Sin embargo, esto ocasionaría un caos debido a que estamos trabajando con una secuencia de probabilidades que es igual al producto de otras probabilidades a posteriori, y si una de estas es 0, toda la secuencia tendrá una probabilidad 0. Es por esto que se aplican técnicas de suavizado, como por ejemplo, el suavizado de Laplace, el cual consiste en sumar 1 al numerador, y sumar el tamaño del vocabulario en el denominador. Esto permitirá que siga siendo una distribución de probabilidad.

6. Gráficas decodificadoras.

El modelo acústico evaluaba las tramas o frames de entrada. El modelo de lenguaje asignaba una probabilidad a secuencias de palabras. Para unir estos modelos, hace falta definir el grafo decodificador. Es una función que va desde la secuencia de etiquetas acústicas hacia las secuencias de palabras ($G : A \times W$).

La gramática

En computación existen las máquinas de estado finito, las cuales son modelos matemáticos que representan de manera abstracta computación. Las máquinas de estado finito pueden ser divididas, en general, en: aceptadores, transductores, clasificadores y secuenciadores, pero en el reconocimiento del habla sólo nos enfocamos en los primeros dos. También, cabe aclarar, que para cada uno de los cuatro tipos de máquina de estado finito los podemos dividir en uno determinista y en otro no determinista. Para cada no determinista, hay una versión del mismo con los mismos estados determinista.

Un autómata finito determinista es una quíntupla: $(Q,\Sigma ,\delta ,q_{0},F)$

• $Q$ es un un conjunto finito de estados.
• $\Sigma$ es un conjunto finito de símbolos llamado alfabeto.
• $\delta$ es una función de transición $\delta : Q \times \Sigma \rightarrow Q$
• $q_{0}$ es un estado inicial, donde $q_{0} \in Q$
• $F$ es el conjunto de estados de aceptación $F \subseteq Q$

Dentro de los sistemas de reconocimiento de voz, todo el vocabulario que aprendimos en nuestro modelo de lenguaje es el vocabulario en el AFD ($\Sigma$), y el número de estados dependerá del largo de las frases que aprendimos y el tamaño del vocabulario. La gramática de nuestro reconocedor de voz, entonces podrá verse de la siguiente manera:

Donde nuestro estado inicial implicitamente es el primer estado que aparece en la definición de la gramática, es decir $s_{0}$, y el estado de aceptación (solo hay uno en los sistemas de reconocimiento de habla actuales) es el último definido en la gramática, también $s_{0}$.

El léxico de pronunciación

Un Transductor de estado finito (TEF) es una máquina de estado finito. Se puede definir a partir de la sextupla:

$(\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )$,

donde

• $\Sigma$ es el alfabeto de entrada (finito no vacío)
• $\Gamma$ es el alfabeto de salida (finito no vacío)
• $S$ es el conjunto de estados (finito no vacío)
• $s_{0}$ es el estado inicial tal que $s_{0} \in S$
• $\delta$ es una función de transición tal que: $\delta : S \times \Sigma \rightarrow S$
• $\omega$ es una función de salida.

Notemos que $\omega, \Gamma$ son elementos que no pertenecen a la quintupla del AFD, y que los TEF no tienen un conjunto de estados de aceptación.

Está claro que necesitamos asociar a una secuencia de fonemas una palabra (o secuencia de palabras) y a su vez, que una secuencia de palabras implica una secuencia de fonemas. Para ello, utilizaremos los transductores de estado finito. Este mapeo de secuencia de palabras a secuencias de fonos es llamado léxico de pronunciación. Usualmente en el reconocimiento del habla, estos transductores son no-deterministas y pueden hacer transiciones instantáneas de un estado a otro a partir de la cadena vacía o $\epsilon$.

Analicemos la siguiente imagen, que representa un Transductor de Estado Finito de juguete:

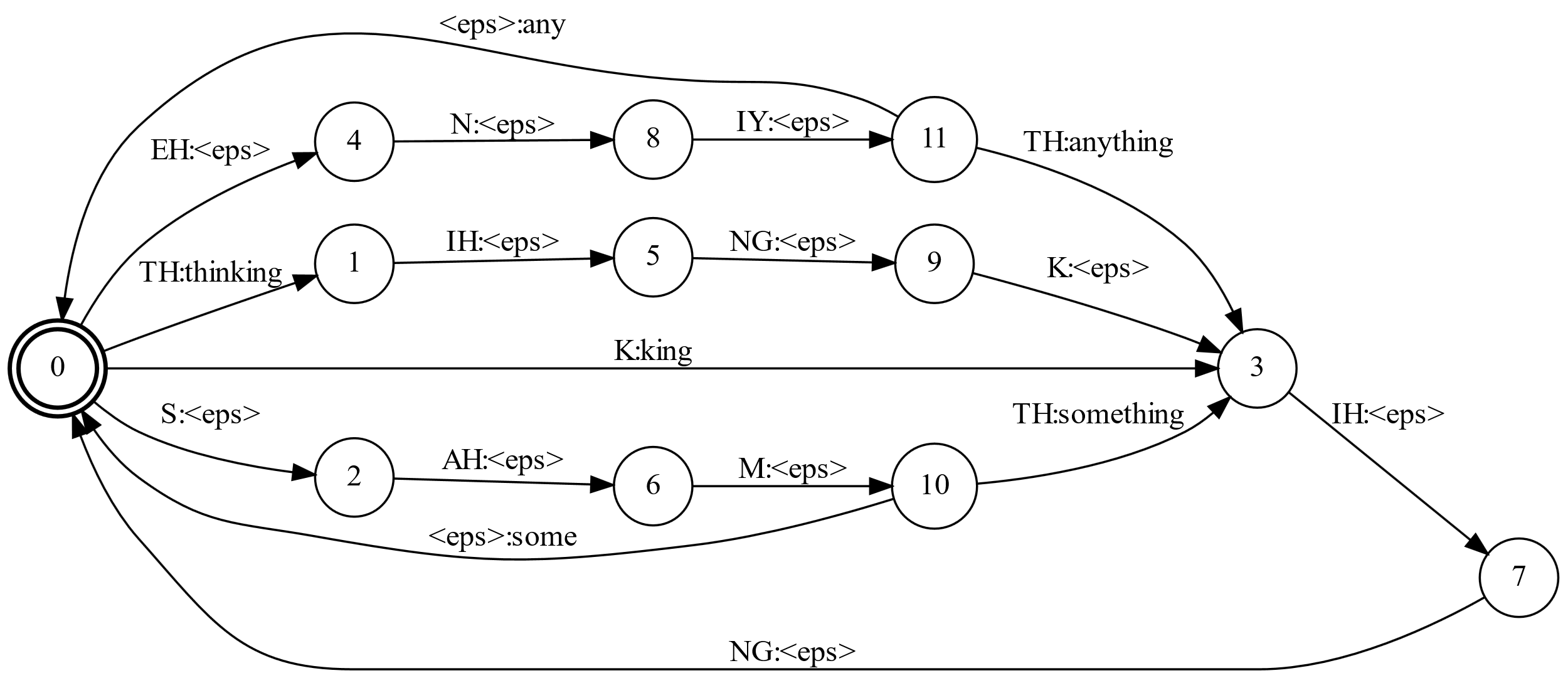
Los arcos en el grafo se definen por la notación $\Sigma_{k} : \Gamma_{k}$ donde está claro que $\Gamma_{k} \in \Gamma$, que es el alfabeto de salida. Es decir, el alfabeto de salida de nuestro TEF es una secuencia de palabras y la cadena vacía., y el alfabeto de entrada son los fonos y la cadena vacía. $\omega$ es la función de salida que nos regresa la palabra a partir de la secuencia de fonos de entrada, aunque en el ejemplo anterior puede verse como si fuera un estado de aceptación que regresa la palabra. No es exactamente un aceptador o un autómata, ya que para cada secuencia de fonos regresa una única palabra, aunque cada palabra pueda ser regresada a partir de varias secuencias de fonos. Esto cumple con la definición de función.

¿Y qué pasó con los estados de los HMM?

Nadie se ha olvidado de ellos. Para tratarlos bien, hacemos un TEF que mapee secuencias de los estados de los HMM hacia las secuencias de fonos, mismas que luego pasarán por los TEF que vimos anteriormente.

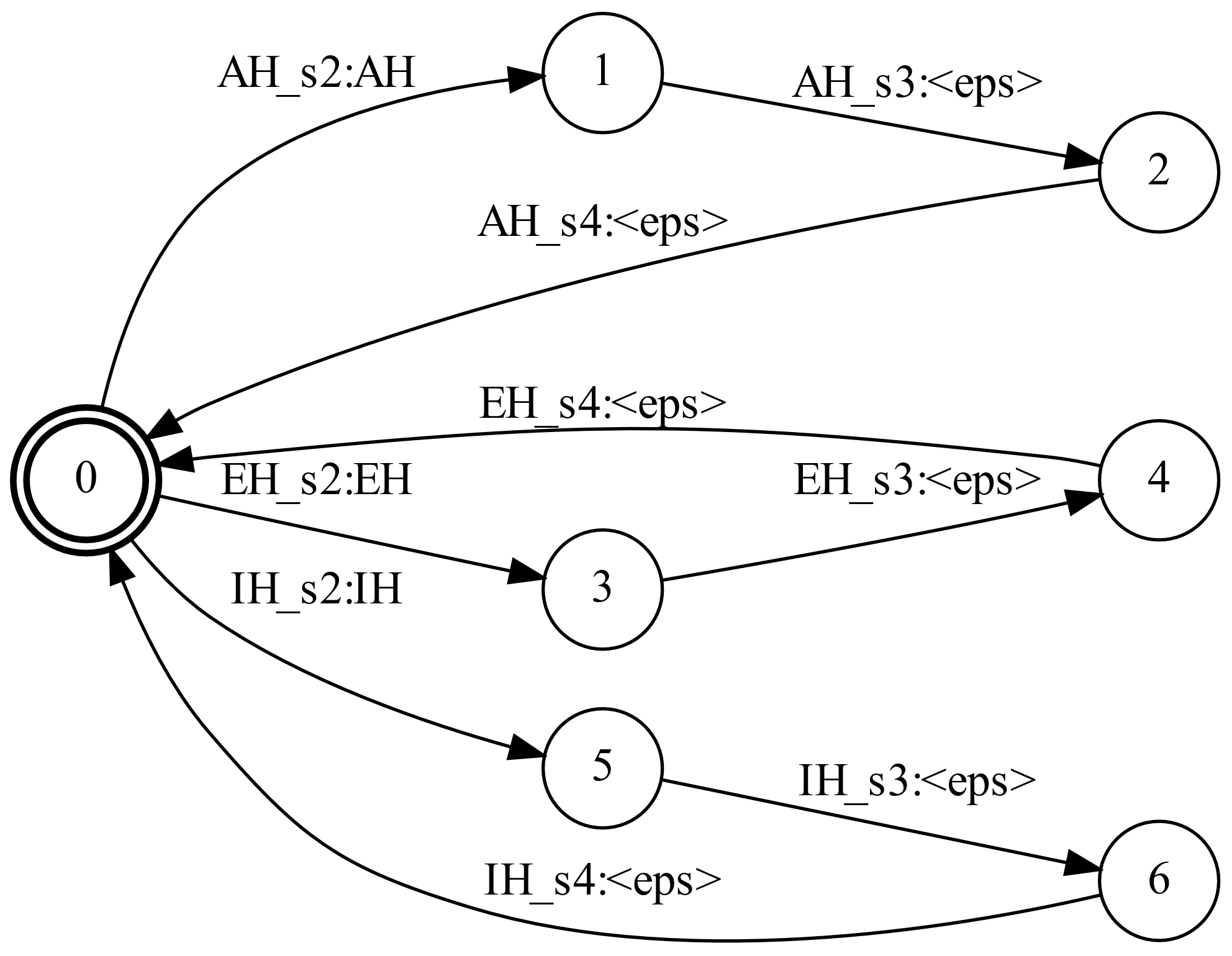
Nótese que ahora las salidas serán los fonos con los que trabajarémos más adelante, pues la secuencia de fonos después nos deberá mapear palabras, como lo vimos anteriormente.

Transductores de estado finito con pesos: Transductor de N-gramas.

Un transductor de estado finito con pesos pone pesos en las transiciones, además de los símbolos de entrada y salida. Aquí podemos encontrar una definición muy seria y formal, que hace uso de términos del álgebra moderna y, por supuesto, de los autómatas (aquí). Como habremos imaginado, en las transiciones de palabras hacia secuencia de palabras, las transiciones irán acompañadas ahoora de un peso, el cual podría ser una probabilidad, o incluso, la perplejidad que le asocia nuestro modelo de N-grama.

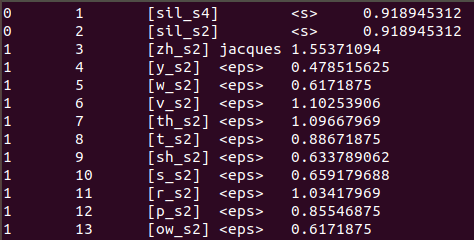
En la imagen anterior, tenemos un Transductor de Estado Finito con Pesos. Cada renglón, representa un arco en la gráfica del transductor. La primer columna es el estado de salida, y la segunda es el estado de llegada. La tercer columna es la entrada (en este caso es una etiqueta que representa toda una secuencia de palabras) y la cuarta es la salida. En los primeros dos renglones vemos dos secuencias diferentes que nos regresan <s>. Ese símbolo representa el inicio de una oración o sentencia. Y en la quinta columna tenemos el peso asociado a este mapeo generado por la perplejidad obtenida en nuestro modelo de lenguaje.

Composición de transductores